논문 선정
강필성 교수님의 비즈니스 어낼리틱스 수업의 다섯번째 논문 구현 주제는 Semi-Supervised Learning이다.
본 포스트에서는 Deep Generative Model을 활용한 Semi-Supervised Learning의 방법론 중 하나인 Categorical GAN을 다루고자 한다.
Categorical GAN은 아래의 논문에서 처음 소개되었다.

Springenberg, J. T. (2015). Unsupervised and semi-supervised learning with categorical generative adversarial networks. arXiv preprint arXiv:1511.06390.
모든 데이터가 Unlabled Data일 경우 Unlabled Data의 분포 가 포함되어 있는 경우 입력 데이터의 분포 \(P(x)\)를 모델링하는 방법론을 비지도 학습이라고 한다. 이 때 입력 데이터의 분포 \(P(x)\)를 모델링하는 방법은 크게 Generative model과 Discriminative model로 나뉜다. 전자의 경우 분포를 직접 예측하는 방법론이지만 후자는 이 분포를 직접 예측하는 대신 데이터를 잘 구별하기 위해 \(P(x)\)를 구하지 않고 잘 분류된 클래스 간의 거리를 최대화를 하는 것을 주 목적으로 한다. 이 때 만약 일부 데이터가 Labled Data라면 Labled Data의 정보를 활용한 Semi-supervised Learning 방식을 적용하여 성능을 향상 시킬 수 있다. 오늘 소개할 Categorical GAN은 Semi-supervised Learning 방식 중 하나로 Generative model과 Discriminative model의 각각 개별적인 특성을 결합하여 성능을 향상시킨 모델이다.
GAN
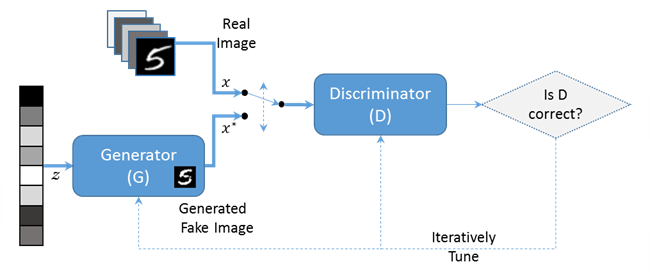
Generative Adversarial Networks(GAN)은 대표적인 Generative model 중 하나이다. 학습 데이터를 통해 GAN을 학습시키면 입력 데이터의 분포 \(P(x)\)를 학습하여 학습 데이터와 비슷한 분포를 갖는 데이터를 생성시킬 수 있다. GAN은 크게 Generator와 Discriminator로 구성되어 있다. 학습 과정에서 random noise를 입력으로 받는 Generator는 이를 학습 데이터와 유사하게 만들도록 학습을 진행한다. 반면 Discriminator는 Generator가 생성한 가짜 데이터를 진짜 학습 데이터와 구분하는 역할을 한다. 이를 모델의 손실함수를 Discriminator와 Generator가 경쟁적으로 학습을 시키면 Generator는 진짜와 거의 같은 수준의 데이터를 생성할 수 있고, Discriminator는 분별 성능이 점차 향상되게 된다. 결과적으로 학습이 완료된 모델에서 Generator는 입력 데이터의 분포 \(P(x)\)와 유사한 \(P_{model}(x)\)을 학습하게 된다.
RIM
앞서 설명했듯이 Categorical GAN은 Generative model과 Discriminative model의 특징을 결합하였다고 했다. GAN 자체가 Generative model이니 Categorical GAN이 어떤 Discriminative model의 특징은 활용했는지가 Categorical GAN의 메인 아이디어라고 할 수 있다. Categorical GAN은 Discriminative Clustering을 수행하는 Regularized Information Maximization(RIM) 모델의 Discriminative model 특성을 활용했다. RIM은 Clustering 기법 중 하나로 클래스를 나누는 Decision Boundary에 데이터가 없도록 하면서 클래스가 고르게 배치될 수 있도록 하는 방법론이다. 일반적으로 Decision Boundary에 데이터가 없도록 하게 되면 Cluster의 수, 즉 클래스의 수가 줄게 된다. 반면 전체적으로 클래스가 고르게 배치되도록 하면 모든 데이터 포인트를 각각 다른 클래스로 두었을 때 최적이 될 수 있다.
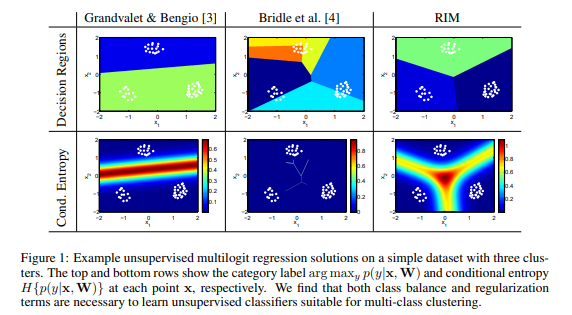
따라서 RIM은 이를 조절하기 위해 Regularization을 활용한다. 즉, RIM의 메인 아이디어는 이렇게 Decision Boundary에 데이터가 없도록 하면서도 클래스가 늘어나 모든 데이터 포인트를 각각 다른 클래스로 되지는 않게 하는 Regularization에 있다.

Categorical GAN
Categorical GAN은 앞서 설명한 일반적인 GAN과 달리 Discriminator가 단순히 Generator에서 생성된 가짜 데이터와 진짜 데이터를 구분하는 것 이상으로 어떤 클래스인지까지 구분할 수 있도록 디자인되었다. 이때 Discriminator가 구분하는 클래스는 진짜 데이터의 클래스(\(C_1,C_2,\ldots,C_N\))와 Generator가 생성한 \(C_{fake}\)로 총 \(N+1\)개의 클래스를 구분한다. 일부 데이터만 Label이 있는 Semi-supervised Leaning Task에서 Categorical GAN의 Generator는 가짜 데이터를 생성하는 과정을 통해 \(P(y|x)\)를 모방하여 Unlabled Data의 Label을 예측하는 \(P(y|x_u)\)의 생성에 도움을 준다. 또한 Discriminator의 경우 클래스를 구분하므로 일반적인 Classifier와 동일한 구조를 가지고 있지만 Generator와의 경쟁학습을 통해 더욱 강화된 성능을 지니게 된다.
이제 Categorical GAN에서 RIM의 아이디어를 가지고 온 부분을 살펴보면 RIM의 Regularization 함수와 같이 Categorical GAN에서는 Generator가 Discriminator에 대해 Regularization 역할을 하여 Discriminator가 클래스를 잘 분류하게끔 학습하는 역할을 한다.
Categorical GAN은 RIM에서 엔트로피를 활용한 목적 함수를 구성한 것과 같이 조건부 엔트로피를 목적함수로 활용한다.
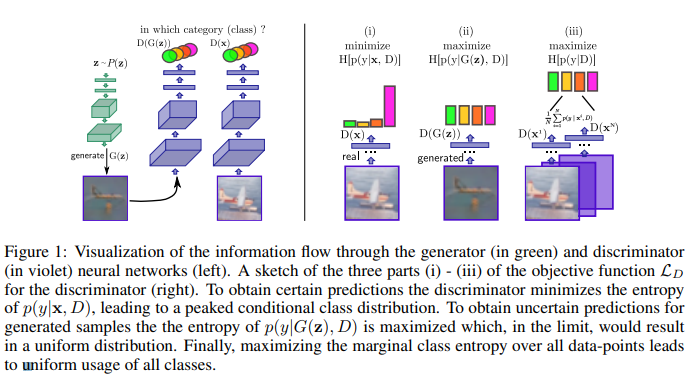
Generator \(G(z)\)와 Discriminator \(D(\cdot)\)으로 구성되어 있고 이때 \(H\)가 조건부 엔트로피이다.
먼저 Discriminator \(D(\cdot)\)는 진짜 데이터는 진짜 데이터의 클래스(\(C_1,C_2,\ldots,C_N\))를 확실하게 구분을 할 수 있어야 하기 때문에 위 그림의 (i)와 같이 각 클래스 데이터가 입력되면 특정 클래스에만 속할 확률이 높게 나와야 되므로 엔트로피가 낮아야 한다. 따라서 진짜 데이터에 대해서는 엔트로피 \(H[p(y|x,D)]\)를 최소화해야 한다. 다음으로 Generator에서 생성된 가짜 데이터(\(G(z)\))의 경우 어떤 진짜 데이터의 어떤 클래스에도 속하지 않고 가짜로 구별되어야 하기 때문에 그림의 (ii)과 같이 모든 클래스의 확률이 고르게 나와야 하므로 엔트로피 \(H[p(y|G(z),D)]\)는 커져야 한다. 다음으로 그림 (iii)은 학습 데이터의 모든 클래스가 균일하게 뽑혔을 것이라는 가정으로 입력 데이터 \(x\)에 대한 Marginal Distribution의 엔트로피 \(H[p(y|D)]\)는 최대화되어야 한다.
다음으로 Generator \(G(z)\)는 생성한 가짜 데이터가 Discriminator를 속일 정도로 입력 데이터와 비슷하게 되도록 학습을 해야 되므로 생성된 각 클래스별 생성 데이터는 각 클래스에 높은 확률로 속하도록 학습이 이루어져야 한다. 즉 Discriminator와 마찬가지로 엔트로피 \(H[p(y|x,G(z))]\)를 최소화하도록 학습이 되어야 한다. 다음으로 Discriminator의 그림 (iii) 케이스와 동일하게 생성된 샘플은 어떤 클래스에 치우치지 않고 고르게 분포해야 하므로 \(H[p(y|D)]\)는 최대화되어야 한다.
이를 모두 합친 손실함수는 다음과 같다.
\[L_{D}=\max_{D}{H_{\chi}[p(y|D)]-E_{x \sim \chi}[H[p(y|x,D)]]+E_{z \sim p(z)}[H[p(y|G(z),D)]]}\] \[L_{G}=\max_{G}{H_{G}[p(y|D)]+E_{z \sim p(z)}[H[p(y|G(z),D)]]}\]이 때 \(L_{D}\)의 마지막 항은 모든 \(z\)에 대해 조건부 엔트로피를 구할 수 없기 때문에 몬테카를로 방법을 쓴다. 즉 \(p(z)\)로부터 M개를 뽑아 이를 \(G(z)\)에 넣어 평균을 계산하는 방식이다.
Code
Code 수행은 MNIST 데이터를 활용하여 Categorical GAN을 학습시킨 코드이다. 먼저 라이브러리와 데이터를 불러오는 코드는 다음과 같다.
import math
import random
import numpy as np
import matplotlib.pyplot as plt
import torch
import torch.nn as nn
import torch.nn.functional as F
import torch.optim as optim
import torchvision
import torchvision.transforms as transforms
import torchvision.utils as vutils
from PIL import Image
train_set = torchvision.datasets.MNIST(root=PATH,train=True,
download=True,transform=transform)
train_loader = torch.utils.data.DataLoader(train_set,batch_size=batch_size,
shuffle =True, num_workers=workers)
test_set = torchvision.datasets.MNIST(root=PATH,train=False,
download=True, transform=transform)
test_loader = torch.utils.data.DataLoader(test_set, batch_size=batch_size,
shuffle = False, num_workers=workers)
train_iter = iter(train_loader)
test_iter = iter(test_loader)
먼저 Categorical GAN의 Generator Network와 Discriminator Network를 구성하면 다음과 같이 구성할 수 있다.
class Generator(nn.Module):
def __init__(self):
super(G,self).__init__()
self.fclayer1 = nn.Linear(latent_size,out_features)
self.bnlayer1 = nn.BatchNorm2d(32*4)#4x4
self.upsamplelayer2 = nn.Sequential(nn.ConvTranspose2d(in_channels,out_channels,kernel_size,stride=stride,padding=padding),
nn.BatchNorm2d(out_channels,momentum=0.1,eps=1e-5),
nn.ReLU())
self.up_sample_layer3 = nn.Sequential(nn.ConvTranspose2d(in_channels,out_channels,kernel_size,stride=stride,padding=padding),
nn.BatchNorm2d(out_channels,momentum=0.1,eps=1e-5),
nn.ReLU())
self.up_sample_layer4 = nn.Sequential(nn.ConvTranspose2d(in_channels,out_channels,kernel_size,stride=stride,padding=padding),
nn.BatchNorm2d(out_channels,momentum=0.1,eps=1e-5),
nn.ReLU())
self.tanh = nn.Tanh()
def forward(self, x):
x = self.fclayer1(x)
x = x.view(-1,32*4,4,4)
x = self.bnlayer1(x)
x = self.upsamplelayer2(x)
x = self.upsamplelayer3(x)
x = self.upsamplelayer4(x)
x = self.tanh(x)
return x
class Discriminator(nn.Module):
def __init__(self):
super(D,self).__init__()
self.downsamplelayer1 = nn.Sequential(nn.Conv2d(in_channels,out_channels,kernel_size,stride=stride,padding=padding),
nn.LeakyReLU(0.2))# 14x14
self.downsamplelayer2 =nn.Sequential(nn.Conv2d(in_channels,out_channels,kernel_size,stride=stride,padding=padding),
nn.LeakyReLU(0.2))#7x7
self.downsamplelayer3 = nn.Sequential(nn.Conv2d(in_channels,out_channels,kernel_size,stride=stride,padding=padding),
nn.LeakyReLU(0.2))
self.fc_layer4 = nn.Linear(latent_size,out_features)
self.softmax = nn.Softmax(dim=-1)
def forward(self, x):
x = self.downsamplelayer1(x)
x = self.downsamplelayer2(x)
x = self.downsamplelayer3(x)
x = torch.flatten(x,1)
x = self.fclayer4(x)
x = self.softmax(x)
return x
이제 구축된 네트워크를 Categorical GAN의 목적함수를 통해 학습시키기 위해 앞서 설명한 조건부 엔트로피 목적함수를 디자인하기 위한 함수를 정의한다.
\[L_{D}=\max_{D}{H_{\chi}[p(y|D)]-E_{x \sim \chi}[H[p(y|x,D)]]+E_{z \sim p(z)}[H[p(y|G(z),D)]]}\] \[L_{G}=\max_{G}{H_{G}[p(y|D)]+E_{z \sim p(z)}[H[p(y|G(z),D)]]}\]Labled data를 보유하고 있을 때는 Semi-supervised Learning Task를 수행하기 위해 Discriminator Network의 목적함수에 크로스엔트로피 텀을 추가할 수 있다.
\[L_{D}=\max_{D}{H_{\chi}[p(y|D)]-E_{x \sim \chi}[H[p(y|x,D)]]+E_{z \sim p(z)}[H[p(y|G(z),D)]]+\lambda E_{(x,y) \sim \chi^L}[CE[y,p(y|x,D)]]}\]class MarginalH(nn.Module):
def __init__(self):
super(MarginalH, self).__init__()
def forward(self, x):# NxK
x = x.mean(axis=0)
x = -torch.sum(x*torch.log(x+1e-6))
return x
class JointH(nn.Module):
def __init__(self):
super(JointH, self).__init__()
def forward(self, x):
x = -x*torch.log(x+1e-6)
x = 1.0/batch_size*x.sum()
return x
G_net = Generator().to(device)
D_net = Discriminator().to(device)
jointH = JointH()
marginalH = MarginalH()
G_optimizer = optim.Adam(G_net.parameters(),lr=1e-4,betas=(0.5,0.9))
D_optimizer = optim.Adam(D_net.parameters(),lr=1e-4,betas=(0.5,0.9))
구축한 모델의 initial weight을 적당히 주고 학습하지 않은 Generator 네트워크의 노이즈 \(z\)로 생성된 결과물을 확인해보면 다음과 같다.
noise_z = torch.randn(batch_size, latent_size,device=device) # noise z
G_net.apply(weights_init)
D_net.apply(weights_init)
with torch.no_grad():
fake_batch=G_net(noise_z)

for ep in range(epochs):
for i, (data, target_y) in enumerate(train_loader):
b_size=data.shape[0]
data = data.to(device=device)
#Train Discriminator
D_net.zero_grad()
y_real = D_net(data)
joint_entropy_real = jointH(y_real)#minimize uncertainty
marginal_entropy_real = marginalH(y_real)#maximize uncertainty
z = torch.randn(b_size,latent_size).to(device=device)#uniform distribution sampling
fake_images = G_net(z)
y_fake = D_net(fake_images.detach())
joint_entropy_fake = jointH(y_fake)#maximize uncertainty
ce = torch.nn.CrossEntropyLoss()
cross_entropy = ce(y_real, target_y)
loss_D = joint_entropy_real - marginal_entropy_real - joint_entropy_fake + l*cross_entropy
loss_D.backward(retain_graph=True)
D_optimizer.step()
#Train Generator
G_net.zero_grad()
y_fake = D_net(fake_images)
marginal_entropy_fake = marginalH(y_fake)#maximize uncertainty
joint_entropy_fake = jointH(y_fake)#maximize uncertainty
loss_G = joint_entropy_fake-marginal_entropy_fake
loss_G.backward(retain_graph=True)
G_optimizer.step()
이제 모델이 학습이 완료된 후에 학습된 Generator 네트워크의 노이즈 \(z\)로 생성된 결과물을 확인해보면 다음과 같다.
noise_z = torch.randn(batch_size, latent_size,device=device) # noise z
with torch.no_grad():
fake_batch=G_net(noise_z)

결론
논문에서 제시하는 실험결과에 따르면 MNIST 데이터에서 적은 수의 데이터만 Label을 가지고 Semi-supervised Learning을 실행했을 때도 테스트 에러가 매우 낮게 나온다.
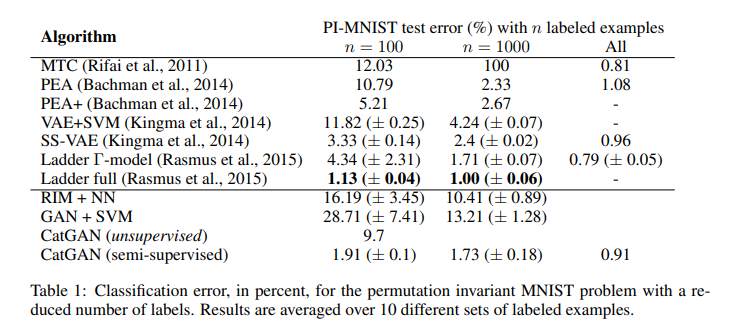
하지만 실제 모델을 구축하여 결과를 확인하니 full-labeled data로 학습을 하여도 충분한 성능을 못 얻었다. 하이퍼 파라미터 세팅이 부족하여 생기는 결과일 수도 있으므로 추후 모델을 계속 다듬어 볼 예정이다. 또한 논문 구현 과정에서 Semi-supervised Learning Task를 수행하기 위해 목적함수에 추가하는 항인 크로스엔트로피 텀을 Discriminator Network의 loss에 추가하는 과정에서 오류가 있을 것이라 생각되어 다시 점검을 해봐야 될 것 같다.
\[L_{D}=\max_{D}{H_{\chi}[p(y|D)]-E_{x \sim \chi}[H[p(y|x,D)]]+E_{z \sim p(z)}[H[p(y|G(z),D)]]+\lambda E_{(x,y) \sim \chi^L}[CE[y,p(y|x,D)]]}\]참고문헌
- Springenberg, J. T. (2015). Unsupervised and semi-supervised learning with categorical generative adversarial networks. arXiv preprint arXiv:1511.06390.
- Krause, A., Perona, P., & Gomes, R. G. (2010). Discriminative clustering by regularized information maximization. In Advances in neural information processing systems (pp. 775-783).