논문 선정
강필성 교수님의 비즈니스 어낼리틱스 수업의 두번째 논문 구현 주제는 Kernel-based Leanring이다. Kernel-based Method 중 Gaussian Process를
이 기회를 통해 이해하고자 아래의 논문을 선정하였다.

Ebden, M. Gaussian Processes for Regression: A Quick Introduction (Robotics Research Group, University of Oxford, 2008)
MOTIVATION
다음과 같이 독립 변수 \(x\)의 특정 값에서 종속 변수 \(y\)에 대해 노이즈가 있는 관측치가 주어졌을 때
\[\mathcal{D} = [(\mathbf{x}_1, y_1) \dots (\mathbf{x}_n, y_n)]\] \[\mathbf{x} \in \mathbb{R}^D\] \[y \in \mathbb{R}\]일반적인 회귀 문제는 각 관측 값 \(y\)는 함수 \(f(x)\)와 가우시안 분포를 따르는 노이즈로 분해할 수 있다.
\[y = f(x) + \epsilon\] \[\epsilon \sim \mathcal{N}(0, \sigma_n^2)\]이를 통하여 새로운 데이터 포인트 \(x_*\)가 주어지면 해당하는 종속 변수 \(y_*\)에 대한 최적의 추정치를 찾아낼 수 있다. 만일 함수 \(f(x)\)가 선형임을 가정한다면 최소제곱법을 사용하여 최적의 추정치를 찾아내는 선 \(f(x)\)를 구할 수 있다 (선형 회귀). 하지만 대개의 경우 \(x\)와 \(y\)가 선형의 관계를 띈다는 선형 모델의 가정이 유효하지 않으므로 입력 데이터 \(x\)를 더 높은 차원의 공간에 투영한 다음 선형 모델을 적용한다.
\[\mathbf{\phi(x)} \in \mathbb{R}^M \, ,where \, M>D\] \[y = f(\phi(x)) + \epsilon\] \[\epsilon \sim \mathcal{N}(0, \sigma_n^2)\]예를 들어 \(\phi(x)\)를 2차, 3차 또는 nonpolynomial 함수를 사용하면 보다 고차원 공간에서 다항식 회귀를 수행할 수 있다. 하지만 이렇게 복잡한 함수의 회귀를 수행할 수 있게끔 하는 함수 \(f(\phi(x))\)를 어떻게 선택해야 할지의 문제가 남아 있다. 가우시안 프로세스는 이 기저함수가 특정한 모델 (eg. \(f(x)=mx+c\)))을 가진다는 가정 대신에 데이터가 기저함수의 정확한 형태에 영향을 끼치도록 보다 일반적이고 유연한 방식으로 함수를 표현할 수 있게끔 한다. 즉, 가우시안 프로세스는 기저함수를 명시적으로 지정할 필요가 없다.
DEFINITION OF A GAUSSIAN PROCESS
가우시안 프로세스는 다변량 가우시안 분포를 무한 차원으로 확장한 형태이다.
예를 들어 무한 차원의 벡터를 연속형 값을 인풋으로 받아 인덱싱된 값들을 반환하는 일종의 함수로 생각해보자.
이 개념을 무한 차원의 다변량 가우시안 분포에 적용하면 이것이 바로 가우시안 프로세스이다.
가우시안 프로세스에서 얼핏 무한한 함수 공간상에서 분포를 고려하는 것이 쉽지 않아 보이지만 실제로 가우시안 프로세스는 Training Dataset과
Test Dataset의 데이터 포인트들에 해당하는 입력 포인트 \(x_n\)의 유한 집합 내에서의 함숫값만을 고려하면 된다.
보다 쉽게 말하면 우리가 보유하고 있는 각 n개의 관측치 \(y = (y_1 \dots y_n)\)는 일부 \(n\) 변량의 다변량 가우시안 분포에서
샘플링된 단일 점으로 생각할 수 있다. 이를 거꾸로 추론하는 것이 가우시안 프로세스이다.
다변량 가우시안 분포는 단일 유한 차원 평균 벡터와 단일 유한 차원 공분산 행렬에 의해 완전히 지정되지만 가우시안 프로세스에서는 정의된 유한 부분 집합에 대한 다변량 가우시안 분포가 여러 차원을 가질 수 있기 때문에 이를 활용할 수 없다. 대신 각 요소별 평균 함수 \(m(x)\)와 요소별 공분산 함수(커널 함수) \(k(x, x\prime)\)로 가우시안 프로세스를 나타낸다.
\[m(x) = E[f(x)]\] \[k(x, x\prime) = E[f(x_i)-m(x_i)(f(x_j)-m(x_j))]\]다시 앞선 일반적인 회귀 문제의 모형을 생각해보자. 회귀 문제의 목표는 데이터가 주어졌을 때 이를 표현하는 어떤 함수 \(f(x)\)를 학습하고 찾아내는 것이다. 가우시안 프로세스는 평균 함수와 공분산 함수를 통해 \(f(x)\)의 분포를 정의한다.
\[f(x) \sim GP(m(x), k(x, x\prime))\]Training Dataset과 Test Dataset의 유한한 데이터 집합의 각 요소별 평균 벡터와 공분산 행렬은 이 \(m(x)\)와 \(k(x, x\prime)\)의 요소별 값을 이용하여 쉽게 구할 수 있다. 즉, \(\mathbf{f} = (f_{\mathbf{x}_1}, \dots f_{\mathbf{x}_n})\)는 \(\mathbf{f} \sim \mathcal{N}(\bar{\mathbf{f}}, K(X, X))\)으로 나타낼 수 있다.
\[\bar{\mathbf{f}} = \begin{pmatrix} m(\mathbf{x}_1) \\ \vdots \\ m(\mathbf{x}_n) \end{pmatrix}\] \[K(X, X) = \begin{bmatrix} k(\mathbf{x}_1, \mathbf{x}_1) & \ldots & k(\mathbf{x}_1, \mathbf{x}_n) \\ \vdots & \ddots & \vdots \\ k(\mathbf{x}_n, \mathbf{x}_1) & \ldots & k(\mathbf{x}_n, \mathbf{x}_n) \end{bmatrix}\]대부분의 경우 평균 함수로 얻을 수 있는 정보는 별로 없기에 가우시안 프로세스의 평균 \(m(x)\)를 단순한 설정을 위해 0으로 가정하므로 하나의 관측치를 다른 관측치와 연결시켜 파라미터를 추론해야 하는 것은 공분산 함수 \(k(x, x\prime)\) 뿐이다. 논문에서는 공분산 함수의 형태를 Squared Exponential를 사용했고 이는 \(x\)와 \(x\prime\)이 유사한 값을 가질 수록 최대 허용 공분산 \(\sigma_f^2\)에 수렴하는 함수이다. 즉, \(x\)와 \(x\prime\)이 유사하여 \(k(x, x\prime)\)이 최대 허용 공분산이 되면 \(f(x)\)와 \(f(x\prime)\)는 완벽한 상관관계를 지닌다고 해석할 수 있다. 반대로 새로운 \(x\) 값이 추가될 때 먼 곳에 있는 관측값들은 큰 영향을 미칠 수 없도록 \(x\)와 \(x\prime\)이 멀어질 때 \(k(x, x\prime)\)은 0에 수렴하도록 구성되어 있다.
\[k(x, x\prime) = \sigma_f^2 exp( - \frac{( x - x\prime)^2}{2l^2} )\]REPRODUCTION
먼저 코드 구현을 위해 가우시안 프로세스 regression의 전체 골격을 잡아두자
code1
class GPR():
def __init__(self, kernel, optimizer='L-BFGS-B', noise_var=1e-8):
self.kernel = kernel
self.noise_var = noise_var
self.optimizer = optimizer
def sample_prior(self, X_test, n_samples):
pass
def sample_posterior(self, X_test, n_samples):
pass
def log_marginal_likelihood(self, theta=None, eval_gradient=None):
pass
def optimize(self, theta, X_train, y_train):
pass
def _cholesky_factorise(y_cov):
pass
def _sample_multivariate_gaussian(y_mean, y_cov):
pass
Kernel functions
다음으로 가우시안 프로세스의 구성요소 중 가장 중요한 커널 함수 \(k(x, x\prime)\)를 구현을 해보자. 논문에서 사용한 커널 함수인 Squared Exponential 외에 Linear Kernel과 Periodic Kernel을 모두 구현하였다. 각 커널 함수는 모두 symmetric positive semi-definite 공분산 행렬을 구성한다. 코드를 살펴보면 theta 변수와 bounds 변수를 통해 커널 파라미터 \(l\)과 \(\sigma_f^2\)를 조절하도록 하였다. 또한 요소별 공분산 행렬을 for 루프를 통해 구현할 수 있지만 보다 효율적으로 계산하기 위해 numpy 자료형에 최적화된 scipy의 pdist와 cdist를 통해 구현하였다. scipy 의 cdist 함수는 두 개의 자료형 A, B 를 받아서 AxB의 모든 페어에 대한 계산 결과를 2차원 배열로 리턴하고 pdist는 한 자료 안에서 객체 간의 pairwise distance를 리턴한다.
Linear :
\[k(\mathbf{x}_i, \mathbf{x}_j) = \sigma_f^2\mathbf{x}_i^T \mathbf{x}_j\]Squared Exponential :
\[k(\mathbf{x}_i, \mathbf{x}_j) = \text{exp} \left(\frac{-1}{2l^2} (\mathbf{x}_i - \mathbf{x}_j)^T (\mathbf{x}_i - \mathbf{x}_j)\right)\]Periodic :
\[k(\mathbf{x}_i, \mathbf{x}_j) = \text{exp}\left(-\sin(2\pi f(\mathbf{x}_i - \mathbf{x}_j))^T \sin(2\pi f(\mathbf{x}_i - \mathbf{x}_j))\right)\]code2
from scipy.spatial.distance import pdist, cdist, squareform
class Linear():
def __init__(self, signal_variance=1.0, signal_variance_bounds=(1e-5, 1e5)):
self.theta = [signal_variance]
self.bounds = [signal_variance_bounds]
def __call__(self, X1, X2=None):
if X2 is None:
K = self.theta[0] * np.dot(X1, X1.T)
else:
K = self.theta[0] * np.dot(X1, X2.T)
return K
class SquaredExponential():
def __init__(self, length_scale=1.0, length_scale_bounds=(1e-5, 1e5)):
self.theta = [length_scale]
self.bounds = [length_scale_bounds]
def __call__(self, X1, X2=None):
if X2 is None:
# K(X1, X1) is symmetric so avoid redundant computation using pdist.
dists = pdist(X1 / self.theta[0], metric='sqeuclidean')
K = np.exp(-0.5 * dists)
K = squareform(K)
np.fill_diagonal(K, 1)
else:
dists = cdist(X1 / self.theta[0], X2 / self.theta[0], metric='sqeuclidean')
K = np.exp(-0.5 * dists)
return K
class Periodic():
def __init__(self, frequency=1.0, frequency_bounds=(1e-5, 1e5)):
self.theta = [frequency]
self.bounds = [frequency_bounds]
def __call__(self, X1, X2=None):
if X2 is None:
# K(X1, X1) is symmetric so avoid redundant computation using pdist.
dists = pdist(X1, lambda xi, xj: np.dot(np.sin(self.theta[0] * np.pi * (xi - xj)).T,
np.sin(self.theta[0] * np.pi * (xi - xj))))
K = np.exp(-dists)
K = squareform(K)
np.fill_diagonal(K, 1)
else:
dists = cdist(X1, X2, lambda xi, xj: np.dot(np.sin(self.theta[0] * np.pi * (xi - xj)).T,
np.sin(self.theta[0] * np.pi * (xi - xj))))
K = np.exp(-dists)
return K
Sampling from the GP prior
가우시안 프로세스에서 함수를 샘플링하려면 먼저 샘플링된 함수를 평가할 입력 지점 \(n_*\)을 정해주고 해당하는 \(n_*\) 변량의 다변량 가우시안 분포에서 추출해야 한다. 이는 아직 관찰된 데이터를 고려하지 않았기 때문에 커널 함수에 대한 사전 정보가 부족한 가우시안 프로세스 사전 분포에서의 추출을 뜻한다.
\[\mathbf{f}_* \sim \mathcal{N}\left(\mathbf{0}, K(X_*, X_*)\right).\]또한 앞선 언급하였듯 가우시안 프로세스의 평균 함수 \(m(x)\)는 평균 함수로부터 얻을 수 있는 정보가 별로 없기에 단순한 설정을 위해 0으로 가정하였다. 그리고 \(X_*\)로부터 각 커널함수를 적용하여 공분산 행렬 \(K(X_*, X_*)\)를 각각 구성한다. 각 커널 함수는 모두 symmetric positive semi-definite 공분산 행렬을 구성하므로 Cholesky decomposition를 통해 이를 분해할 수 있다.
\[K(X_*, X_*)=LL^T\]다음으로 Cholesky decomposition의 분해 결과에서 가우시안 분포의 샘플 \(\mathbf{z} \sim \mathcal{N}(\mathbf{m}, K)\)를 생성하기 위해 아래의 공식을 활용한다.
\[\mathbf{u} \sim \mathcal{N}(\mathbf{0}, I)\] \[\mathbf{z}=\mathbf{m} + L\mathbf{u}\] \[\mathbb{E}[\mathbf{z}] = \mathbf{m} + L\mathbb{E}[\mathbf{u}] = \mathbf{m}\] \[\text{cov}[\mathbf{z}] = L\mathbb{E}[\mathbf{u}\mathbf{u}^T]L^T = LL^T = K\]이를 코드를 통해 구현하면 아래와 같다.
code3
import numpy as np
def sample_prior(self, X_test, n_samples=1, epsilon=1e-10):
y_mean = np.zeros(X_test.shape[0])
y_cov = self.kernel(X_test)
y_cov[np.diag_indices_from(y_cov)] += epsilon
L = np.linalg.cholesky(y_cov)
u = np.random.randn(y_mean.shape[0], n_samples)
z = np.dot(L, u) + y_mean[:, np.newaxis]
return z
이제 앞서 정의한 세 개의 커널 함수는 각각 다른 가우시안 프로세스 사전분포를 가지므로 이에 따른 각 커널 함수별 가우시안 프로세스 사전분포에서 추출한 샘플들을 추출하면 아래와 같다.
code4
GPR.sample_prior = sample_prior
X_test = np.arange(-5, 5, 0.005)[:, np.newaxis]
sigma_f_sq = 1 # Linear signal_variance
l = 1 # Squared Exponential length_scale
f = 0.5 # Periodic frequency
gps = {'Linear': GPR(Linear(sigma_f_sq)),
'SquaredExponential': GPR(SquaredExponential(l)),
'Periodic': GPR(Periodic(f))}
for name, gp in gps.items():
y_samples = gp.sample_prior(X_test, n_samples=5, epsilon=1e-10)
plt.plot(X_test, y_samples)
plt.title('{} kernel'.format(name))
plt.show()
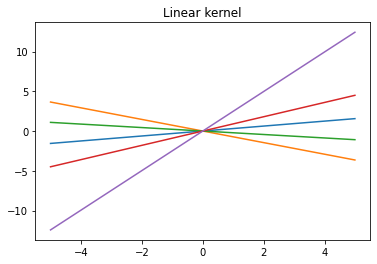
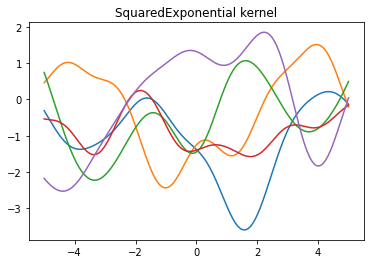

그려진 plot은 각 커널 함수에 해당하는 가우시안 프로세스 사전분포 별로 5개의 함수를 가져온 뒤 이를 그린 결과물이다.
의미있는 예측을 하려면 이렇게 사전 분포로부터 생성될 수 있는 함수 중 관측된 데이터와 일치하는 함수만을 포함하도록 제한해야 한다.
이 과정은 가우시안 프로세스 사후분포로부터 샘플링하는 과정을 통해 이루어 진다.
Sampling from the GP posterior
먼저 가우시안 프로세스 사전분포 하에서 관측치 y는 다음과 같이 정의될 수 있다.
\[\mathbf{y} \sim \mathcal{N}\left(\mathbf{0}, K(X, X) + \sigma_n^2I\right)\]추가된 항인 \(\sigma_n^2I\)는 제일 처음 언급한 내용대로 관측치의 가우시안 분포를 따르는 노이즈다. 노이즈는 각 관측치에 대해 독립이고 동일한 분포로부터 나온 값이므로 \(K(X, X)\)의 대각 요소에만 추가된다. 다음으로 다변량 가우시안 분포의 marginalisation property를 사용하여 가우시안 사전분포를 따르는 \(\mathbf{f_*}\)와 관측치 \(\mathbf{y}\)의 결합분포를 구하면 다음과 같다.
\[\begin{bmatrix} \mathbf{y} \\ \mathbf{f}_* \end{bmatrix} = \mathcal{N}\left(\mathbf{0}, \begin{bmatrix} K(X, X) + \sigma_n^2I && K(X, X_*) \\ K(X_*, X) && K(X_*, X_*)\end{bmatrix}\right)\]가우시안 프로세스의 사후 분포는 이 결합분포가 조건부로 주어졌을 때의 \(\mathbf{f}_*\)의 분포이고 다음과 같이 정의된다.
\[\mathbf{f}_* | X_*, X, \mathbf{y} \sim \mathcal{N}\left(\bar{\mathbf{f}}_*, \text{cov}(\mathbf{f}_*)\right),\] \[\bar{\mathbf{f}}_* = K(X_*, X)\left[K(X, X) + \sigma_n^2\right]^{-1}\mathbf{y}\] \[\text{cov}(\mathbf{f}_*) = K(X_*, X_*) - K(X_*, X)\left[K(X, X) + \sigma_n^2\right]^{-1}K(X, X_*)\]앞서 사전 분포로부터 샘플링한 방식과 전체적으로 코드의 구성은 동일하지만 사전 분포의 평균과 공분산 대신 사후 분포의 평균과 공분산을 사용한다. 또한 주어진 데이터로부터 얻어지는 고정된 부분을 \(\mathbf{\alpha}\)와 \(\mathbf{v}\)로 정의하고 미리 계산해둠으로써 코드의 구성을 간결하게 했다.
\[[K(X, X) + \sigma_n^2] = L L^T\] \[\mathbf{\alpha} = \left[K(X, X) + \sigma_n^2\right]^{-1}\mathbf{y} = L^T \backslash(L \backslash \mathbf{y})\] \[\mathbf{v} = L^T [K(X, X) + \sigma_n^2]^{-1}K(X, X_*) = L \backslash K(X, X_*)\] \[\bar{\mathbf{f}}_* = K(X, X_*)^T\mathbf{\alpha}\] \[\text{cov}(\mathbf{f}_*) = K(X_*, X_*) - \mathbf{v}^T\mathbf{v}\]code5
def sample_posterior(self, X_train, y_train, X_test, n_samples=1):
# compute alpha
K = self.kernel(X_train)
K[np.diag_indices_from(K)] += self.noise_var
L = np.linalg.cholesky(K)
alpha = np.linalg.solve(L.T, np.linalg.solve(L, y_train))
# Compute posterior mean
K_trans = self.kernel(X_test, X_train)
y_mean = K_trans.dot(alpha)
# Compute posterior covariance
v = np.linalg.solve(L, K_trans.T) # L.T * K_inv * K_trans.T
y_cov = self.kernel(X_test) - np.dot(v.T, v)
y_cov[np.diag_indices_from(y_cov)] += epsilon
L = self._cholesky_factorise(y_cov)
u = np.random.randn(y_mean.shape[0], n_samples)
z = np.dot(L, u) + y_mean[:, np.newaxis]
return z, y_mean, y_cov
관측치를 커널 함수가 Squared Exponential인 가우시안 프로세스 사전분포로부터 랜덤하게 10개를 샘플링한 후, 가우시안 프로세스 사후분포를 정의하여 샘플링하면 아래의 결과와 같다.
code6
GPR.sample_posterior = sample_posterior
gp = gps['SquaredExponential']
# 사전분포로부터 Data generation
X_train = np.sort(np.random.uniform(-5, 5, 10))[:, np.newaxis]
y_train = gp.sample_prior(X_train)
y_train = y_train[:, 0]
plt.plot(X_train[:, 0], y_train, 'r+')
plt.title('Observations')
plt.show()

code7
f_star_samples, f_star_mean, f_star_covar = gp.sample_posterior(X_train, y_train, X_test, n_samples=10)
pointwise_variances = f_star_covar.diagonal()
error = 1.96 * np.sqrt(pointwise_variances) # 95% confidence interval
plt.plot(X_test, f_star_mean, 'b')
plt.fill_between(X_test[:, 0], f_star_mean - error, f_star_mean + error, alpha=0.3)
# Plot samples from posterior
plt.plot(X_test, f_star_samples)
# Also plot our observations for comparison
plt.plot(X_train[:, 0], y_train, 'r+')
plt.title('Posterior samples')
plt.show()
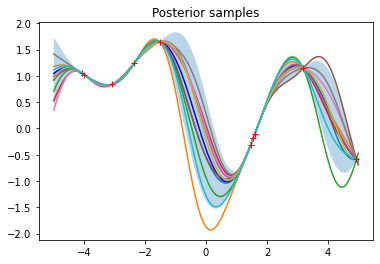
그려진 plot은 사후분포로부터 생성된 함수의 95% 신뢰구간을 나타낸다. 이 plot으로부터 기존의 관측치에서 새로운 데이터가 멀리 벗어날수록 예측은 사전 분포에 대한 영향을 잃고 함수 값의 분산이 증가하는 것을 알 수 있다. 또한 사후분포로부터 생성된 함수들은 모두 관측치를 지나는 것처럼 보이는데 이는 관측치에 대한 노이즈를 매우 작은 값(\(10^{-8}\))으로 설정했기 때문이다. 이 관측치에 대한 노이즈 값 부분은 코드 구성을 살펴보면 알 수 있듯이 직접 설정하여 바꿀 수도 있다.
이렇게 관측치를 사전분포로부터 추출하면 당연히 사전분포를 형성하는 커널 함수가 데이터에 적합한 커널 함수가 될 수 밖에 없다. 그러나 실제 관측치는 이렇게 정의된 사전분포에 딱 떨어진 값이 아니다. 그래서 최적의 커널 함수를 찾는 것 역시 가우시안 프로세스의 중요한 과제이다. 이는 이 포스트의 가장 앞 단락에서 설명한 함수 \(f(\phi(x))\)를 어떤 함수로 가져가야 주어진 데이터를 가장 잘 설명할 수 있을까에 대한 문제와 비슷하다. 하지만 가우시안 프로세스로부터 생성된 커널 함수의 집합은 기저함수의 집합보다 훨씬 광범위한 함수 분포를 포함하기 때문에 최적의 커널 함수를 찾지 못하는 것은 최적의 기저함수를 찾지 못하는 것보다 상대적으로 덜 위험한 결과를 보인다.
다음으로 커널 함수를 잘 선정했더라도 커널 파라미터를 어떻게 결정해야 할지의 문제가 남아 있다. Squared Exponential 커널 함수에서도 커널 파라미터 \(l\)과 \(\sigma_f^2\)를 조절함에 따라 결과가 달리 나타난다. 이는 베이즈 정리를 통하여 해결할 수 있다. 베이즈 정리에 의해 커널 파라미터 \(\theta\)에 대한 사후 분포는 다음과 같이 정의된다.
\[p(\pmb{\theta}|\mathbf{y}, X) = \frac{p(\mathbf{y}|X, \pmb{\theta}) p(\pmb{\theta})}{p(\mathbf{y}|X)}.\]\(\theta\)에 대한 maximum a posteriori (MAP)는 해당 사후 분포 \(p(\pmb{\theta}|\mathbf{y}, X)\)가 가장 클 때 발생한다. 일반적으로 커널 파라미터는 사전 정보가 거의 없기 때문에 커널 파라미터에 대한 사전분포는 uniform 분포를 가정한다. 이 경우 \(\theta_{MAP}\)는 Marginal Likelihood를 최대화하여 구할 수 있다. 실제로 연산을 할 때는 편의를 위해 Log Marginal Likelihood를 최대화하는 \(\theta\)가 \(\theta_{MAP}\)이다.
\[p(\mathbf{y}|X, \pmb{\theta}) = \mathcal{N}(\mathbf{0}, K(X, X) + \sigma_n^2I)\] \[\text{log}p(\mathbf{y}|X, \pmb{\theta}) = -\frac{1}{2}\mathbf{y}^T\left[K(X, X) + \sigma_n^2I\right]^{-1}\mathbf{y} - \frac{1}{2}\text{log}\lvert K(X, X) + \sigma_n^2I \lvert - \frac{n}{2}\text{log}2\pi\]앞선 사후 분포 파트의 코드 구성에서 Log Marginal Likelihood 구성 식 중 데이터로부터 얻어지는 고정 값 \(\mathbf{\alpha}\) 부분은 미리 계산해두었다. (\(\mathbf{\alpha} = \left[K(X, X) + \sigma_n^2\right]^{-1}\mathbf{y} = L^T \backslash(L \backslash \mathbf{y})\)) 남은 부분은 Cholesky decomposition을 통해 \([K(X, X) + \sigma_n^2] = L L^T\)로 분해하여 아래와 같이 전개함으로써 계산을 편리하게 바꾼다.
\[\lvert K(X, X) + \sigma_n^2 \lvert = \lvert L L^T \lvert = \prod_{i=1}^n L_{ii}^2 \quad \text{or} \quad \text{log}\lvert{K(X, X) + \sigma_n^2}\lvert = 2 \sum_i^n \text{log}L_{ii}\]이를 코드를 통해 구성하면 다음과 같다. 코드 구성 상 편의를 위해 log marginal likelihood에 -1을 곱하여 이를 최소화시키는 파라미터를 찾도록 수정하였다.
code8
def log_marginal_likelihood(self, X_train, y_train, theta, noise_var=None):
if noise_var is None:
noise_var = self.noise_var
# Build K(X, X)
self.kernel.theta = theta
K = self.kernel(X_train)
K[np.diag_indices_from(K)] += noise_var
# Compute L and alpha for this K (theta).
L = self._cholesky_factorise(K)
alpha = np.linalg.solve(L.T, np.linalg.solve(L, y_train))
# Compute log marginal likelihood.
log_likelihood = -0.5 * np.dot(y_train.T, alpha)
log_likelihood -= np.log(np.diag(L)).sum()
log_likelihood -= K.shape[0] / 2 * np.log(2 * np.pi)
return log_likelihood
def optimize(self, X_train, y_train):
def obj_func(theta, X_train, y_train):
return -self.log_marginal_likelihood(X_train, y_train, theta)
results = minimize(obj_func,
self.kernel.theta,
args=(X_train, y_train),
method=self.optimizer,
jac=None,
bounds=self.kernel.bounds)
# Store results of optimization.
self.max_log_marginal_likelihood_value = -results['fun']
self.kernel.theta_MAP = results['x']
return results['success']
success = gp.optimize(X_train, y_train)
이제 Squared Exponential 커널 함수의 커널 파라미터 \(\pmb{\theta}=\{l\}\)에 대한 \(\pmb{\theta}_{MAP}\)를 계산하면 \(\pmb{\theta}_{MAP}\)는 1.31723513이고 Maximised log marginal liklehihood는 1.32706104로 나타난다. 물론 이 값이 전역 최적해라 할 수는 없다. 하지만 \(\pmb{\theta}_{MAP}\)는 일반적으로 좋은 추정치이며 데이터를 생성하는데 사용되는 \(\pmb{\theta}\)에 매우 가까운 값이라는 것을 알 수 있다. 또한 위의 코드에서는 보다 간단한 예시를 위해 \(l\)에 대해서만 추정을 진행하기 위해 관측치의 노이즈에 대한 값을 고정 값(\(10^{-8}\))으로 두었지만 커널 파라미터 \(\sigma_n^2\)에 대해서도 동일한 과정을 적용하면 \(\sigma_n^2\)의 추정치를 구할 수 있다.
결론
이번 논문 구현 과제를 통해 가우시안 프로세스를 회귀 문제에 적용하는 과정을 설명했다. 하지만 이는 가우시안 프로세스에 대한 단적인 부분에 불과하다. 가우시안 프로세스는 현재 연구가 깊게 이루어진 분야로 오늘 소개한 내용은 기초에 불과하고 이러한 회귀 문제에 적용하는 과정뿐 아니라 분류 문제에 적용하는 과정, 딥러닝 모델에 결합하는 방법론 등 더욱 다양한 부분이 남아 있다. 아직 가우시안 프로세스에 대한 이해가 부족하기에 회귀 문제에 적용하는 과정에 대해서도 모든 내용을 잘 담지는 못 하였으나, 추후 공부를 통해 보다 깊이 있는 내용을 추가적으로 더 다뤄보고 싶다.
참고문헌
- Williams, C. K., & Rasmussen, C. E. (1996). Gaussian processes for regression. In Advances in neural information processing systems (pp. 514-520).
- Ebden, M. (2015). Gaussian processes: A quick introduction. arXiv preprint arXiv:1505.02965.